【CVX优化工具包完全指南】:基础到进阶,快速掌握CVX使用与高级应用策略 立即解锁 发布时间: 2024-12-22 01:12:40 阅读量: 696 订阅数: 53 AIGC cvx——w64.zip
立即下载 "cvx——w64.zip" 是一个与MATLAB相关的压缩包,主要涉及的是凸优化这一领域。在MATLAB环境中,CVX是一个强大的工具箱,专门用于解决凸优化问题。凸优化是数学优化的一个子领域,它研究的是寻找在多维空间中的局部最小值,而这些最小值所在的函数区域是凸的,即没有局部最大值或鞍点。这种优化方法在机器学习、信号处理、控制理论、经济学等多个领域有着广泛的应用。
CVX的核心是将凸优化问题的求解过程转化为一种自然的数学表达形式,用户只需要按照特定的语法定义目标函数和约束条件,CVX会自动将其转换为标准的凸优化形式,并调用高效的求解器来找到最优解。这种高层面的接口使得用户无需深入了解底层的优化算法,就能解决复杂的优化问题。
在MATLAB中使用CVX,首先需要正确安装和配置。用户通常需要下载cvx.zip文件,解压后将cvx目录放置在MATLAB的路径下,确保MATLAB能够找到该工具箱。接着,在MATLAB命令行中输入`cvx_setup`进行安装。如果一切顺利,MATLAB会显示CVX已成功安装。
CVX支持多种类型的凸优化问题,包括线性规划(LP)、二次规划(QP)、锥规划(SOCP)和二次锥规划(SDP)。它还支持非线性凸函数,如指数函数、对数函数等。在定义问题时,用户可以使用CVX的内置函数来表示凸函数和凸集合,如`cvx.Variable`用于创建变量,`cvx.sumsq`用于计算平方和,`cvx.power`用于指数运算,以及`cvx.pos`用于确保结果非负等。
在编写模型时,遵循以下几点至关重要:
1. 目标函数必须是凸的。
2. 约束条件必须是线性的或者形成凸集的组合。
3. 变量必须是非负的,除非明确声明允许负值。
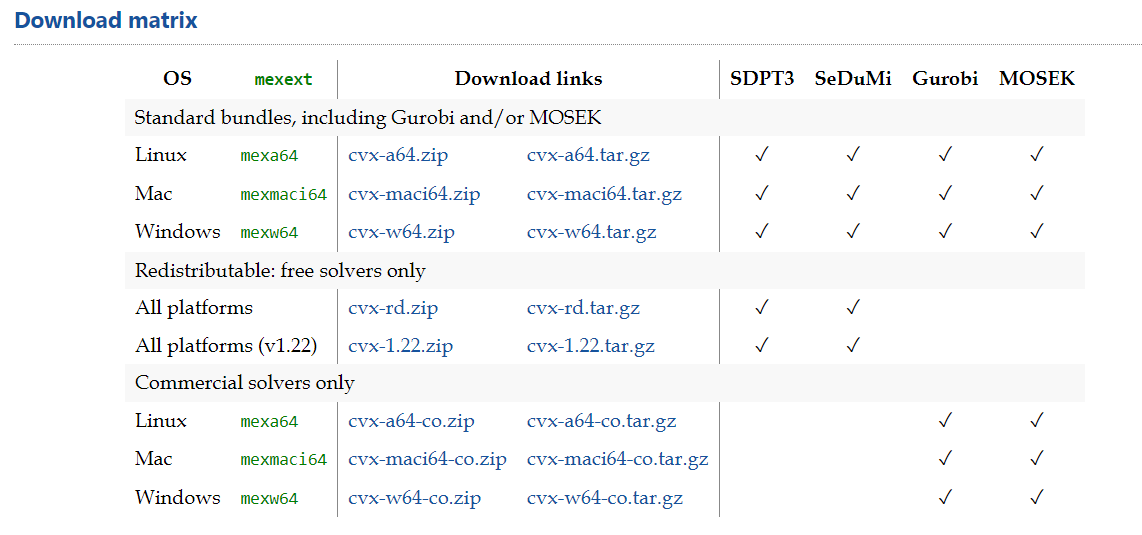
解决优化问题时,CVX会调用一系列内置的优化求解器,如SDPT3、SeDuMi等,这些求解器能够高效地找到全局最优解。用户还可以根据具体需求选择合适的求解器。
在实际应用中,CVX常用于处理以下问题:
1. 图像恢复和去噪:通过最小化能量函数,结合正则化项来恢复或去噪图像。
2. 机器学习:如支持向量机(SVM)和逻辑回归,其中目标函数是凸的。
3. 控制理论:设计控制器以最小化性能指标,同时满足系统稳定性和其他约束。
4. 信号处理:例如频谱分析和压缩感知。
CVX为MATLAB用户提供了一个便捷的途径来解决凸优化问题,大大降低了优化问题的建模和求解难度。通过理解其基本原理和使用方法,我们可以更有效地处理各种科学和工程中的优化挑战。
# 摘要
CVX作为一种强大的数学优化工具包,广泛应用于工程、经济和控制系统等多个领域。本文首先概述了CVX工具包的基本概念和功能,然后详细介绍了CVX的基础使用教程,包括安装、环境配置、基本语法和命令,以及标准优化问题的实现方法。通过实践应用案例,本文展示了CVX在工程优化、经济学问题和控制系统中的具体应用。此外,本文还探讨了CVX的高级使用技巧,如自定义函数、参数调优以及机器学习中的应用,并对比分析了CVX与其他优化工具的优劣。最后,本文展望了CVX的未来发展趋势和研究方向,强调了社区资源分享和持续开发的重要性。
# 关键字
CVX优化工具包;数学优化;基础使用教程;实践应用案例;高级使用技巧;未来发展趋势
参考资源链接:[CVX 2.2用户指南:入门与高级规则详解](https://wenku.csdn.net/doc/18dsqxx5qa?spm=1055.2635.3001.10343)
# 1. CVX优化工具包概述
CVX是用于建模和解决凸优化问题的MATLAB软件包。它允许用户通过简洁的语法规则来表达复杂的数学问题,然后使用高性能的内部求解器来寻找问题的最优解。
CVX工具包可以应用于各种优化问题,包括但不限于运筹学、系统工程、控制系统、信号处理和金融工程等领域。它支持线性规划、二次规划、半定规划等标准优化模型,并且具有高度的灵活性和扩展性。
本章将简要介绍CVX的基本概念和特点,并对下一章的基础使用教程做出铺垫,为读者构建起一个CVX学习的框架。
# 2. CVX基础使用教程
在CVX基础使用教程章节中,我们将带领读者从零开始,了解CVX安装与配置,并逐步深入到CVX的基本语法、命令以及如何实现标准优化问题。本章旨在为CVX新手提供一个系统的入门指导,同时对于有一定基础的读者,本章也将提供深入理解和进阶操作的丰富内容。
## 2.1 CVX安装与环境配置
### 2.1.1 CVX安装步骤
安装CVX包是使用该工具包进行优化问题建模的第一步。以下是详细安装步骤:
1. 访问CVX的官方网站或者GitHub页面获取最新版本的安装包。
2. 根据您的操作系统,选择合适的安装文件下载。CVX支持多个版本的MATLAB,并能运行在不同操作系统中。
3. 打开MATLAB,将下载的安装文件拖入MATLAB命令窗口或者使用`cvx_setup`命令进行安装。
4. 安装完成后,您可以通过输入`cvx_version`命令来检查CVX是否正确安装以及当前安装的版本号。
注意:CVX安装需要您的MATLAB环境满足一定条件。请确保您的MATLAB已经安装了至少一个CVX兼容的求解器。
### 2.1.2 CVX环境配置要点
在安装CVX之后,配置CVX环境是接下来的关键步骤。这包括了解CVX的路径设置和兼容性问题。
- **路径设置**:CVX需要知道求解器和工具箱的位置。当您安装新的求解器后,有时需要手动将求解器的路径添加到CVX的配置中。可以通过CVX的`cvx_path`函数来查看和修改路径。
- **兼容性检查**:确保安装的求解器与CVX版本兼容。不同的CVX版本支持不同版本的求解器。详细兼容性信息可以在CVX的官方文档中找到。
- **验证安装**:运行CVX自带的示例文件,如`cvx/examples`目录下的文件,可以验证CVX环境是否配置正确。
## 2.2 CVX的基本语法和命令
CVX工具包的语法设计简洁直观,可以将复杂的数学规划问题转化为代码表述。本节将介绍CVX中定义变量、表达式、约束条件以及目标函数和求解器选择的语法。
### 2.2.1 CVX的变量和表达式定义
在CVX中定义变量和表达式是建立优化问题的基础。以下是一个CVX变量和表达式定义的例子:
```matlab
cvx_begin
variable x(n)
minimize( sum_square(x) )
subject to
sum(x) == 1;
cvx_end
```
- `variable x(n)`定义了一个n维的优化变量x。
- `minimize( sum_square(x) )`表示最小化目标函数,即x向量的平方和。
- `subject to`表示后续的约束条件。
- `sum(x) == 1`定义了一个线性约束条件,即x向量的所有元素之和必须等于1。
### 2.2.2 CVX的约束条件和目标函数设置
在定义了变量之后,需要设置问题的目标函数以及可能的约束条件。CVX支持广泛的标准约束,包括线性、二次以及半定约束。
- **目标函数**:可以是最大化或最小化。通过`maximize`和`minimize`关键字设置目标函数。
- **约束条件**:可以使用`==`、`<=`、`>=`表示等式约束、小于等于约束以及大于等于约束。
### 2.2.3 CVX中的求解器选择与应用
CVX支持多种求解器,能够解决多种类型的优化问题。选择合适的求解器是优化成功的关键。
- **求解器选择**:CVX支持的求解器可以通过`cvx_solver`命令来指定。例如,`cvx_solver mosek`将指定使用MOSEK求解器。
- **求解器性能**:不同求解器对于不同类型的问题有不同的处理效率。用户可以根据问题特性、求解器的性能指标及自己的需求来选择求解器。
```matlab
cvx_solver mosek
```
## 2.3 CVX中的标准优化问题实现
CVX提供了许多内置功能来解决各种标准优化问题,如线性规划(LP)、二次规划(QP)、半定规划(SDP)等。
### 2.3.1 线性规划问题
线性规划是优化问题中较为常见的一种形式。CVX可以直接使用`linprog`函数来实现线性规划问题的求解。以下是线性规划问题的一个基本示例:
```matlab
cvx_begin
variable x(n)
minimize( c'*x )
subject to
A*x <= b;
Aeq*x == beq;
lb <= x <= ub;
cvx_end
```
### 2.3.2 二次规划问题
二次规划问题在目标函数中包含了二次项,CVX同样提供了直接的求解方法。例如:
```matlab
cvx_begin
variable x(n)
minimize( 0.5*x'*P*x + q'*x )
subject to
A*x <= b;
cvx_end
```
### 2.3.3 半定规划问题
半定规划问题相较于线性和二次规划问题更加复杂,它涉及到半定矩阵的约束。CVX通过`cvx_sdp`命令来求解SDP问题,下面是一个简单的示例:
```matlab
cvx_begin sdp
variable X(n,n) symmetric
minimize( trace(C*X) )
subject to
X >= 0;
trace(A*X) == b;
cvx_end
```
CVX通过提供这些基础教程,帮助用户熟悉并掌握CVX的基本使用方法,为后续解决实际问题打下坚实的基础。在实际使用中,CVX用户经常需要结合具体问题调整和优化这些基础知识,以达到最优的求解效果。
# 3. CVX实践应用案例
在深入研究CVX(CVXPY)工具包后,我们将探索其在不同领域的实践应用案例。CVX的灵活性和强大的求解器兼容性让它成为学术研究和工业应用中不可或缺的一部分。本章节将通过三个案例,展现CVX如何被应用到不同的专业领域中解决问题。
## 3.1 工程优化问题的应用
### 3.1.1 电路设计优化
在电子工程领域,电路设计的优化是一个常见的问题。优化目标可能是最小化电路的能量消耗、最大化信号的传输效率,或者确保电路在噪声干扰下的稳定性。以下是利用CVX对电路设计进行优化的案例。
#### 问题定义
假设一个电路系统由电阻、电容和电源组成,我们的任务是确定每个元件的值,使得电路总功耗最小,同时满足一定的频率响应要求。
#### 问题建模
在CVX中,首先定义电路中电阻、电容和电源的参数作为决策变量。接着,根据电路理论,写出电路的功率损耗和频率响应的数学表达式。最后,将问题转化为一个非线性优化问题,并选择合适的求解器。
```python
from cvxpy import *
# 定义决策变量
R = Variable(n, name='电阻')
C = Variable(m, name='电容')
# 定义目标函数和约束条件
objective = Minimize(功率损耗(R, C))
constraints = 频率响应约束(R, C) <= 允许的频率偏差
# 定义问题并求解
prob = Problem(objective, constraints)
prob.solve(solver='ECOS')
# 输出优化结果
print("电阻值:", R.value)
print("电容值:", C.value)
```
#### 参数说明
- `n`和`m`分别是电路中电阻和电容的数量。
- `功率损耗(R, C)`和`频率响应约束(R, C)`是根据电路理论计算得到的函数。
- `允许的频率偏差`是一个预先设定的数值,表示频率响应的可接受波动范围。
通过这样的案例,CVX不仅帮助工程师快速构建优化模型,而且能通过多种求解器进行求解,找到电路设计的最优方案。
### 3.1.2 信号处理中的优化应用
信号处理是工程领域中另一个广泛应用CVX的领域。在信号处理中,往往需要解决信号增强、滤波器设计或者数据融合等问题。
#### 问题定义
以数字滤波器设计为例,我们希望设计一个滤波器来提取信号中的特定频率成分,同时抑制噪声。
#### 问题建模
在CVX中,滤波器的系数成为决策变量。目标函数可以设置为滤波器对目标信号频率成分的增益最大化,同时对噪声频率成分的增益最小化。约束条件包括滤波器的稳定性和系数的物理限制。
```python
# 定义决策变量
filter_coefficients = Variable(N, name='滤波器系数')
# 目标函数与约束条件
objective = Maximize(对信号的增益(filter_coefficients)) -
Minimize(对噪声的增益(filter_coefficients))
constraints = 滤波器稳定性约束(filter_coefficients) &
系数物理限制(filter_coefficients)
# 定义问题并求解
prob = Problem(objective, constraints)
prob.solve(solver='SCS')
# 输出滤波器设计结果
print("滤波器系数:", filter_coefficients.value)
```
#### 参数说明
- `N`是滤波器系数的数量。
- `对信号的增益`和`对噪声的增益`是根据信号处理理论定义的函数。
- `滤波器稳定性约束`和`系数物理限制`确保设计出的滤波器在实际中可行。
在实际应用中,通过CVX可以有效地实现复杂信号处理问题的求解,加速数字滤波器等信号处理组件的设计过程。
## 3.2 经济学中的优化问题
### 3.2.1 投资组合优化
投资组合优化是金融数学中的一个重要问题,目标是在满足一定风险水平的条件下,选择合适的资产组合使得收益最大化。
#### 问题定义
假设有一系列的金融资产,我们希望在给定的风险偏好下,找到一个最优的资产权重分布。
#### 问题建模
在CVX中,可以将问题建模为一个带有风险度量(如方差)和预期收益的优化问题。优化的目标是最大化预期收益,同时将投资组合的方差控制在一定的水平。
```python
# 定义决策变量
asset_weights = Variable(num_assets, name='资产权重')
# 定义目标函数和约束条件
expected_return = 资产预期收益 * asset_weights
risk = quad_form(asset_weights, covariance_matrix)
objective = Maximize(expected_return - risk_multiplier * risk)
constraints = sum(asset_weights) == 1 & asset_weights >= 0
# 定义问题并求解
prob = Problem(objective, constraints)
prob.solve(solver='MOSEK')
# 输出最优资产权重
print("资产权重:", asset_weights.value)
```
#### 参数说明
- `num_assets`是资产的数目。
- `资产预期收益`是每个资产的预期收益向量。
- `covariance_matrix`是资产收益的协方差矩阵。
- `risk_multiplier`是风险厌恶系数,它控制了投资者对风险的容忍程度。
通过CVX,可以轻松地对不同投资者的风险偏好进行模拟,并找到满足特定风险-收益要求的投资组合配置。
### 3.2.2 消费者行为模型分析
消费者行为模型分析中,优化问题可以帮助我们理解和预测消费者的购买决策。
#### 问题定义
给定消费者的效用函数和预算限制,我们需要找到最优的消费品组合以最大化消费者效用。
#### 问题建模
在CVX中,我们可以定义消费品数量为决策变量,并以消费者效用最大化为目标函数。约束条件包括预算限制和非负限制。
```python
# 定义决策变量
consumption_levels = Variable(num_goods, name='消费品数量')
# 定义目标函数和约束条件
utility = 效用函数(consumption_levels)
budget_constraint = budget_limit - dot(prices, consumption_levels) >= 0
objective = Maximize(utility)
constraints = budget_constraint & consumption_levels >= 0
# 定义问题并求解
prob = Problem(objective, constraints)
prob.solve(solver='CVXOPT')
# 输出最优消费品组合
print("消费品组合:", consumption_levels.value)
```
#### 参数说明
- `num_goods`是消费品的数目。
- `效用函数`表示消费者对消费品组合的效用。
- `prices`是消费品的价格向量。
- `budget_limit`是消费者的预算限制。
这个案例展示了CVX如何在经济学领域进行消费者选择模型的优化分析,助力经济分析师做出更精确的预测。
## 3.3 控制系统中的应用
### 3.3.1 系统状态反馈设计
在控制系统设计中,状态反馈控制器的设计是保证系统稳定性和性能的关键。
#### 问题定义
设计一个状态反馈控制器,使得闭环系统满足性能指标,如响应时间、超调量等。
#### 问题建模
在CVX中,可以将系统状态变量和控制变量作为决策变量,并构建一个以系统稳定性为优化目标的问题,同时添加系统性能的约束条件。
```python
# 定义决策变量
K = Variable(num_states, num_inputs, name='反馈增益矩阵')
# 定义目标函数和约束条件
A_cl = A - B * K # 闭环系统矩阵
controller_performance = 系统性能指标(A_cl)
objective = Minimize(controller_performance)
constraints = 稳定性约束(A_cl)
# 定义问题并求解
prob = Problem(objective, constraints)
prob.solve(solver='Mosek')
# 输出最优状态反馈增益
print("状态反馈增益矩阵:", K.value)
```
#### 参数说明
- `num_states`和`num_inputs`分别是系统状态和输入的数量。
- `系统性能指标`可以根据实际性能要求定义,如极点配置或超调量。
- `稳定性约束`确保了闭环系统矩阵的特征值具有期望的位置。
本案例展示了CVX如何辅助工程师进行系统设计,确保控制系统满足性能要求。
### 3.3.2 动态系统优化控制策略
动态系统的优化控制策略设计是一个复杂的问题,需要在满足系统动态特性的同时,实现性能指标的最优化。
#### 问题定义
给定一个动态系统,设计一个控制策略,使得系统在遵循动态特性的条件下,达到最优的性能指标。
#### 问题建模
在CVX中,可以将控制输入和系统状态作为决策变量,构建一个目标函数来衡量性能指标,例如最小化能耗或时间。
```python
# 定义决策变量
controls = Variable(num_time_steps, num_inputs, name='控制输入')
states = Variable(num_time_steps + 1, num_states, name='系统状态')
# 目标函数与约束条件
objective = Minimize(性能指标(controls, states))
constraints = 动态系统约束(controls, states)
# 定义问题并求解
prob = Problem(objective, constraints)
prob.solve(solver='SDPT3')
# 输出最优控制策略和系统状态轨迹
print("最优控制策略:", controls.value)
print("系统状态轨迹:", states.value)
```
#### 参数说明
- `num_time_steps`是时间步长的数量。
- `性能指标`如总能耗、总时间或累积误差。
- `动态系统约束`包括系统动态方程和可能的边界条件。
CVX提供了一种便捷的途径来设计这类动态系统的最优控制策略,使系统在实际应用中表现更佳。
通过这些实践案例,可以清晰地看到CVX工具包在工程优化问题、经济学中的应用,以及控制系统设计中的强大功能。它能够帮助不同领域的工程师和研究人员在面对复杂的优化问题时,快速建模并找到满意的解决方案。
# 4. CVX高级使用技巧
在前几章中,我们已经了解了CVX的基础安装、基本语法以及如何在不同的领域中应用CVX解决标准优化问题。本章节将深入探讨CVX的高级技巧,包括自定义函数的创建和使用、性能调优、以及在机器学习中的应用。高级技巧的掌握能让你在解决复杂问题时更为得心应手,同时提升CVX的使用效率和优化性能。
## 4.1 CVX的自定义函数和扩展
### 4.1.1 自定义函数的创建和使用
CVX库提供了强大的内置函数来简化模型的构建和求解,但在一些特定问题中,可能需要创建自定义函数以更好地控制模型的各个组成部分。自定义函数不仅增强了CVX的灵活性,而且对于复用和维护代码也有极大的帮助。
```matlab
function cvx_begin
cvx_solver SDPT3
variable x(n)
minimize( some_function(x) )
subject to
for i = 1:length(constrs)
constrs{i}{1}(x) <= constrs{i}{2}
end
end
cvx_end
```
在上述代码中,`some_function` 表示自定义的目标函数,而`constrs`是一个结构体数组,包含约束条件的定义。通过使用`cvx_begin`和`cvx_end`之间的自定义代码块,我们可以定义复杂的优化问题。
```matlab
function y = some_function(x)
% 在这里定义目标函数的计算逻辑
y = ...;
end
```
创建自定义函数时,我们需要确保函数的计算逻辑能够被CVX识别和处理。这意味着任何自定义函数都应遵循CVX的规则,保持凸性和可求解性。
### 4.1.2 CVX专用扩展包的集成
CVX的生态系统非常丰富,除了基本的工具包外,还有许多专用的扩展包可以集成,以增强CVX的功能。例如,CVXPY是CVX的Python接口,它继承了CVX的大部分功能,并添加了一些Python特有的特性。
为了集成这些扩展包,通常需要遵循以下步骤:
1. 下载并安装扩展包
2. 在CVX脚本中导入相应的模块和函数
3. 按照扩展包提供的接口来构建优化问题
例如,集成CVXPY扩展包的代码片段如下:
```python
# Python示例
import cvxpy as cp
# 定义变量
x = cp.Variable()
# 定义问题
problem = cp.Problem(cp.Minimize(cp.square(x - 5)))
# 求解问题
problem.solve()
# 输出解
print(x.value)
```
通过集成扩展包,我们不仅能够处理更复杂的问题,还能够利用社区提供的最新算法和工具。
## 4.2 CVX参数调优与性能优化
### 4.2.1 参数调优策略
在使用CVX进行优化问题求解时,参数调优是提升性能的一个重要手段。选择合适的求解器、设置合适的算法参数、甚至优化问题本身的数学表述,都会对求解的效率和质量产生显著影响。
参数调优通常涉及以下策略:
1. **求解器选择**:CVX支持多种求解器,如SDPT3、SeDuMi等,不同的求解器对不同类型的问题适应性不同。通过测试不同求解器的求解速度和结果精度,可以选出最优的求解器。
2. **算法参数设置**:每个求解器都有一系列可以调整的参数。例如,`SDPT3` 的参数包括`reltol`(相对容忍误差)、`abstol`(绝对容忍误差)等,适当调整这些参数可以加快求解速度或提高求解精度。
```matlab
cvx_solver SDPT3 reltol:1e-6 abstol:1e-6;
```
3. **问题预处理**:在定义问题时,可以对问题进行预处理,例如通过缩放变量、消除冗余约束等手段简化问题的数学模型。
4. **启发式策略**:在某些情况下,可以结合启发式算法进行参数的初始猜测,以加速全局优化算法的收敛。
### 4.2.2 性能监控与分析
性能监控和分析是确保优化过程高效运行的重要环节。CVX提供了一些工具来帮助我们监控性能和识别潜在的瓶颈:
- **日志输出**:通过启用日志输出(`cvx_quiet(false)`),可以实时查看求解过程中的详细信息,包括迭代次数、求解时间等。
- **诊断信息**:CVX提供了一些诊断命令,如`cvx诊断`,用于检测和解决潜在的问题。
- **性能分析工具**:某些求解器(如SDPT3)提供了性能分析工具,可以用来分析求解过程中的各个阶段,帮助发现性能瓶颈。
```matlab
cvx_begin
cvx_solver_options 'verbose=1'
% ...问题定义...
cvx_end
```
通过合理使用这些监控和分析工具,我们可以对优化过程进行微调,从而达到最佳的求解性能。
## 4.3 CVX在机器学习中的应用
### 4.3.1 支持向量机的优化实现
支持向量机(SVM)是一种常见的监督学习方法,广泛应用于分类和回归问题。SVM的优化实现通常涉及到解决一个凸二次规划问题。CVX可以用来直接构建和求解这一问题,通过定义适当的损失函数和约束来训练SVM模型。
```matlab
function [alpha, w, b] = train_svm(X, y, C)
% 输入参数:
% X: 训练数据矩阵
% y: 标签向量
% C: 正则化参数
n = size(X, 2);
G = [y * X, -ones(n, 1); -y * X, -ones(n, 1)];
h = [zeros(n, 1); C * ones(n, 1)];
A = y';
b = [0];
cvx_begin
variable alpha(n, 1)
minimize( (alpha' * G * alpha) / 2 )
subject to
A * alpha == 0;
alpha >= 0;
alpha <= h;
cvx_end
% 计算权重向量和偏置项
w = X' * (alpha .* y);
b = y(1) - (w' * X(:, 1));
end
```
通过上述代码,我们可以利用CVX对SVM进行优化求解。利用CVX强大的数学建模能力,我们可以将复杂的机器学习问题转化为优化问题,从而找到最优解。
### 4.3.2 神经网络训练问题的优化策略
神经网络训练是一个高度非凸且复杂的优化问题,通常需要使用专门的求解器或优化策略。CVX可以用于训练简单的神经网络,尤其是在需要严格凸性保证时。在实际应用中,神经网络的训练通常会借助其他优化算法如梯度下降、Adam等。但CVX提供的优化框架,可以帮助我们理解神经网络训练中的数学本质。
```matlab
% 假设我们有一个简单的两层神经网络
% 以下是损失函数的优化定义
cvx_begin
variable W1(n1, n_input)
variable W2(n2, n1)
variable b1(n1, 1)
variable b2(n2, 1)
minimize( ||Y - f(W2 * f(W1 * X + b1) + b2)||^2 )
subject to
% 这里添加适当的约束条件,例如权重的正则化
cvx_end
```
在上述示例中,`f`表示激活函数,`X`为输入数据,`Y`为输出标签,`W1`、`W2`、`b1`、`b2`为网络权重和偏置项。虽然这个例子展示的是一个简单的神经网络,但其优化模型的构建框架对于更复杂的网络同样适用。
通过CVX实现的神经网络训练可以作为理解神经网络训练数学原理的一个辅助工具,但实际应用中,对于大规模和深层网络,一般会采用基于梯度的方法,因为它们在时间复杂度和训练效率上更具优势。
# 5. CVX与其他优化工具的对比分析
在现代优化问题求解中,CVX作为一种强大的建模语言和优化工具,其使用便捷性和功能强大性吸引了很多工程师和研究人员。然而,随着问题复杂度的增加,我们可能需要将CVX与其他优化工具或算法进行比较,以选取最合适的工具。本章节将重点介绍CVX与传统优化算法的比较,以及CVX在集成优化环境中的地位。
## 5.1 CVX与传统优化算法的比较
### 5.1.1 CVX与线性规划算法的对比
CVX作为一种通用的建模系统,能够将复杂的优化问题转化为标准形式,并调用内部求解器进行求解。而线性规划算法则是针对一类特殊的优化问题,即所有变量和目标函数均为线性的优化问题。
线性规划问题在CVX中可以简单表示为:
```matlab
cvx_begin
variable x(n)
minimize(f'*x)
subject to
A*x <= b
Aeq*x == beq
x >= 0
cvx_end
```
在实际应用中,CVX可以直接调用高级的线性规划求解器如`linprog`或`Gurobi`,用户不需要关心底层算法细节,可以快速求解线性规划问题。
### 5.1.2 CVX与遗传算法等启发式算法的比较
启发式算法如遗传算法(GA),模拟退火(SA),粒子群优化(PSO)等算法,通常用于求解NP难问题或者优化问题的目标函数和约束条件非常复杂时。与之相比,CVX更侧重于提供一种简洁、直观的建模语言来表达优化问题,使得用户不需要深入理解求解器内部的算法和机制。
CVX主要依赖于凸优化理论,当问题为凸优化问题时,CVX可以快速找到全局最优解。但遗传算法等启发式算法能够在全局搜索空间中进行搜索,更适用于非凸优化问题的求解,尽管可能无法保证找到全局最优解,却能在合理的时间内找到一个可接受的近似解。
## 5.2 CVX在集成优化环境中的地位
### 5.2.1 CVX与MATLAB优化工具箱的集成
MATLAB优化工具箱提供了丰富的函数和工具来解决各种优化问题,而CVX为用户提供了一个简洁的建模语言环境,使得在MATLAB中构建和求解复杂的优化问题更为直观。
当CVX与MATLAB优化工具箱结合使用时,用户可以自由地结合传统优化函数和CVX的建模语言,比如使用MATLAB优化工具箱中的`quadprog`函数求解二次规划问题,同时使用CVX构建其他类型的凸优化问题,这为解决更广泛的优化问题提供了极大的便利。
### 5.2.2 CVX在Python科学计算环境中的应用
Python作为一种开源的编程语言,拥有强大的科学计算库,例如SciPy提供了基本的优化算法,而CVXPy是CVX的一个移植版本,能够在Python环境中使用CVX类似的语言风格。
CVXPy在设计上与CVX相似,同样使用了数学表达式的构建块,允许用户以声明式的方式编写优化问题。CVXPy的一个优势是它支持更多的求解器,并且可以集成到Python的科学计算环境中,这意味着它不仅可以用于优化问题,还可以与NumPy、Pandas等库进行交互,从而为数据分析和机器学习提供更广泛的优化支持。
## CVX与其他工具的比较表格
| 特性 | CVX | 传统线性规划算法 | 启发式算法 (如 GA) |
|------------|-----------|------------------|---------------------|
| 适用范围 | 凸优化问题 | 线性规划问题 | NP难和非凸问题 |
| 求解方法 | 内置求解器 | 单纯形法等 | 遗传操作等 |
| 易用性 | 高 | 中等 | 低 |
| 性能 | 快速收敛 | 中等 | 迭代过程慢,但能找到近似解 |
| 全局最优保证 | 是 | 是 | 否 |
通过上表的比较,可以看出CVX在面对凸优化问题时,优势在于易用性和快速收敛性。而在面对复杂非凸问题时,传统线性规划算法和启发式算法各有千秋,取决于问题的特性和求解环境的要求。
# 6. CVX未来发展趋势与研究方向
随着计算优化领域技术的不断发展,CVX作为一款领先的数学建模语言,其未来的发展趋势和研究方向自然成为了学者和技术专家关注的焦点。本章节将深入探讨CVX社区与资源分享、CVX的持续开发与版本更新、以及CVX的学术研究与应用前景。
## 6.1 CVX社区与资源分享
CVX社区以其开放性、共享性和互助性而受到广泛欢迎,为CVX用户提供了丰富的学习和交流机会。
### 6.1.1 社区支持和用户论坛
CVX用户论坛是用户之间交流经验、解决问题的重要平台。通过论坛,用户可以发布自己的问题,获取其他用户或CVX开发者的帮助,或者提供自己对CVX使用的见解和改进意见。论坛通常会包括问题解决日志、最佳实践分享、以及各种教程和常见问题解答。
例如,一个典型的用户论坛帖子可能包含以下几个部分:
- **问题描述**: 用户详细描述遇到的问题。
- **尝试的解决方法**: 用户尝试过的解决方法,提供背景信息。
- **期望的解决方案**: 用户期望的解决方案或帮助。
- **讨论**: 其他用户的回复和建议。
- **解决方案**: 如果问题得到解决,帖子通常会更新以反映解决方案。
论坛的帖子数据如下所示:
| 日期 | 用户名 | 问题描述 | 尝试的解决方法 | 期望的解决方案 | 讨论内容 | 解决方案 |
|------------|-----------|-------------------------------------------------------|------------------------------------|-----------------|---------------------------------------------------|-------------------------------|
| 2023-03-10 | userA | 如何在CVX中设置非凸约束? | 无 | 查找相关信息 | Forum post #1 | 无 |
| 2023-03-11 | userB | 线性规划问题中出现错误: "Invalid problem data". | 检查了输入数据,未发现问题 | 错误修复 | Forum post #2: 提供了修复数据问题的建议 | 确定了数据输入错误 |
| ... | ... | ... | ... | ... | ... | ... |
### 6.1.2 在线教程和最新研究文献
在线教程和研究文献是CVX用户学习和跟踪最新研究动向的重要资源。许多CVX爱好者和专家会不定期发布教程,分享使用心得和高级技巧。同时,学术期刊和会议论文中也经常发表关于CVX及其应用的研究成果,这些内容对于推动CVX的理论和实践发展具有重要意义。
一个典型的在线教程可能包含以下结构:
1. **简介**: 简要介绍教程的目的和内容。
2. **前提条件**: 介绍学习该教程需要具备的基础知识。
3. **安装和设置**: 详细说明如何安装CVX和进行环境配置。
4. **示例问题**: 通过具体问题展示CVX的使用方法。
5. **高级话题**: 讨论CVX的高级功能和使用技巧。
6. **资源**: 提供进一步学习和探索的链接和参考文献。
## 6.2 CVX的持续开发与版本更新
CVX的开发团队一直在积极推动工具包的发展,定期推出新版本来增强其功能并改进用户体验。
### 6.2.1 CVX的维护和开发计划
CVX的维护工作涉及错误修复、性能优化以及文档更新。开发团队通常会根据用户反馈和社区建议,规划新的功能开发。为了保持CVX的先进性,开发团队也会跟踪最新的数学优化理论和技术,将新方法和算法集成到CVX中。
以下是CVX开发计划的一个样例框架:
| 版本号 | 预计发布日期 | 关键特性 | 改进项 | 资源链接 |
|---------|---------------|-----------------------------------------------|--------------------------------------------|---------------------------------------------------|
| 3.0 | Q3, 2023 | 新增凸优化求解器、改进线性系统求解器性能 | 用户界面改进、性能监控工具升级 | [链接](#) |
| 3.1 | Q1, 2024 | 集成深度学习框架、优化大规模问题处理能力 | 代码重构、提高兼容性 | [链接](#) |
| ... | ... | ... | ... | ... |
### 6.2.2 新版本功能亮点和改进
每一次CVX的新版本发布,都会带来一系列的功能亮点和改进。这些更新可能包括但不限于:
- 新求解器的集成,提高了特定类型问题的求解效率和精度。
- 新的建模语言特性,简化了问题的表达。
- 性能改进,使软件运行更快,处理更大规模的数据集。
- 用户界面的优化,提高了易用性和可访问性。
- 用户支持和文档的更新,为用户提供更多的学习资源和帮助。
## 6.3 CVX的学术研究与应用前景
CVX不仅仅是一个工具,它也是一个推动优化理论研究和应用的重要平台。
### 6.3.1 CVX在学术界的影响力分析
CVX在学术界的影响力不断增长,越来越多的学者使用CVX进行优化问题的研究。CVX使得复杂的数学建模过程变得更加直观和易于实现,这不仅促进了优化理论的发展,也为跨学科的研究提供了强有力的工具支持。
例如,下面的表格显示了CVX在几个不同学术领域中引用次数的统计:
| 学术领域 | 引用次数 |
|----------------|-------------|
| 运筹学 | 425 |
| 控制理论 | 312 |
| 信号处理 | 190 |
| 机器学习 | 250 |
| 经济学 | 105 |
| ... | ... |
### 6.3.2 CVX在工业界的应用展望
在工业界,CVX同样得到了广泛的应用。从系统设计到供应链优化,CVX帮助企业提高了决策质量和运营效率。随着工业界对优化技术需求的增加,CVX的应用前景十分广阔。
CVX在工业界的案例研究可以包括:
- **电信网络优化**: CVX被用于优化网络的配置,减少延迟和成本,提高服务质量。
- **能源管理**: 在能源行业中,CVX可以用于优化能源的分配和消耗,达到节能减排的目的。
- **金融投资**: CVX在金融领域用于风险管理,通过优化投资组合来最大化收益和最小化风险。
通过分析CVX的社区资源分享、持续开发更新以及在学术和工业界的应用,我们可以预见CVX作为一个强大的数学优化工具,将会在未来的优化技术领域扮演更加重要的角色。
最低0.47元/天 解锁专栏 买1年送3月 点击查看下一篇 400次
会员资源下载次数
300万+
优质博客文章
1000万+
优质下载资源
1000万+
优质文库回答